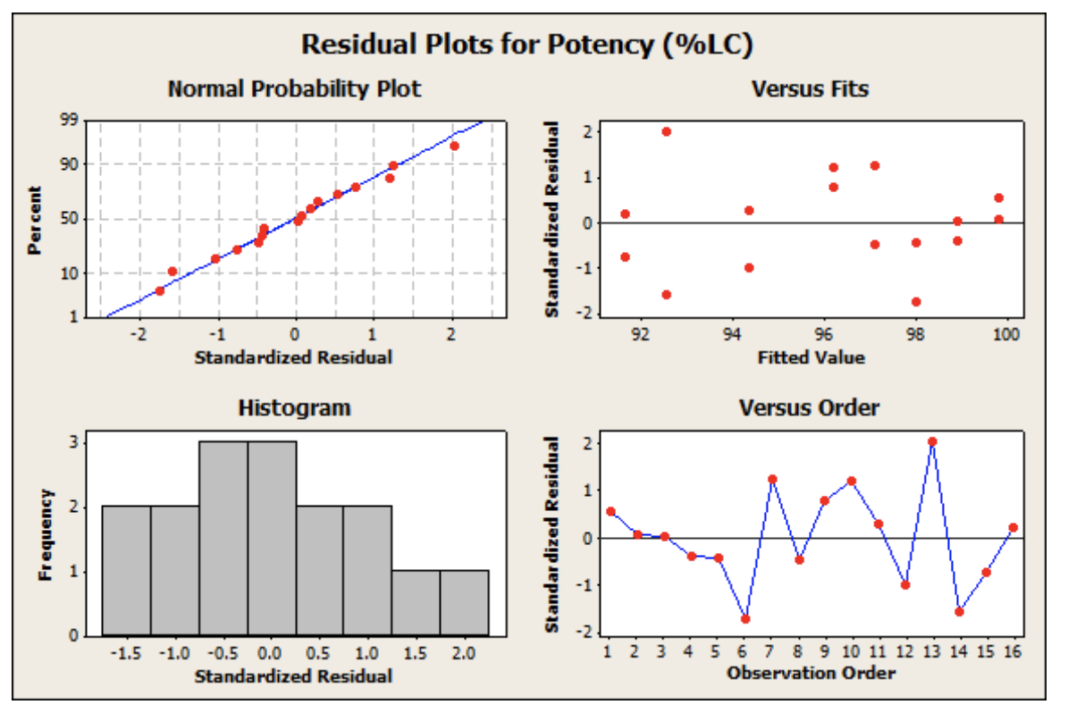
In the realm of data analysis, understanding the nuances of residual analysis can offer profound insights into complex data trends. Residual analysis is a powerful tool that helps analysts and researchers discern patterns, assess model performance, and make informed decisions based on their data. This article delves into advanced techniques in residual analysis, shedding light on how these methods can enhance data interpretation and improve analytical outcomes.
What is Residual Analysis?
Residual analysis involves examining the residuals, or the differences between observed values and the values predicted by a model. By analyzing these residuals, one can determine whether a model is appropriately capturing the underlying trends in the data. Residuals can reveal discrepancies, biases, and areas where the model may need refinement.
Why Advanced Techniques are Essential
While basic residual analysis is valuable, advanced techniques can offer deeper insights and more precise evaluations. These techniques are particularly useful in complex data scenarios where traditional methods might fall short. Here’s a closer look at some advanced approaches:
1. Quantile Regression Residual Analysis
Quantile regression residual analysis extends the traditional residual analysis by evaluating the model’s performance across different quantiles of the data. This technique helps in understanding how well the model performs at various points of the distribution, not just the mean. It’s particularly useful in dealing with heteroscedasticity and outliers, providing a more comprehensive view of residual behavior.
2. Residual Plots and Smoothing Techniques
Residual plots are graphical representations of residuals versus predicted values or other variables. Advanced techniques in this area include using smoothing methods such as LOWESS (Locally Weighted Scatterplot Smoothing) to identify non-linear patterns and trends that might not be apparent in standard residual plots. These smoothed residual plots can help in diagnosing model mis-specifications and uncovering subtle data patterns.
3. Bootstrap Methods for Residual Analysis
Bootstrap methods involve resampling the residuals to estimate the variability and stability of model parameters. By generating multiple resamples, analysts can assess the robustness of their model and the reliability of the residuals. This technique is particularly useful in scenarios where traditional assumptions may not hold or when dealing with small sample sizes.
4. Spatial Residual Analysis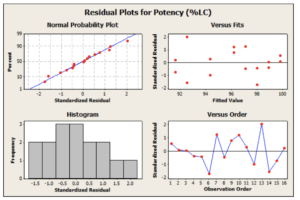
In spatial data analysis, residuals can exhibit spatial dependence that traditional residual analysis might overlook. Spatial residual analysis involves examining residuals in the context of their spatial locations to identify any spatial patterns or correlations. This technique is crucial in fields such as environmental studies and geographical data analysis, where spatial relationships play a significant role.
5. Time-Series Residual Analysis
For time-series data, residual analysis can be extended to consider autocorrelation and temporal dependencies. Advanced techniques in this domain include examining autocorrelation plots of residuals to detect serial correlations and employing advanced time-series models to address any identified issues. This ensures that the model adequately captures temporal trends and seasonality.
Best Practices for Effective Residual Analysis
To maximize the benefits of residual analysis, consider the following best practices:
- Ensure Model Assumptions: Validate that the assumptions of your chosen model are met before diving into residual analysis. This includes checking for linearity, homoscedasticity, and normality of residuals.
- Use Multiple Techniques: Employ a combination of residual analysis techniques to gain a comprehensive understanding of model performance and residual behavior.
- Visualize Data: Utilize graphical methods to visualize residuals and trends. Visualizations can often reveal patterns and issues that might not be apparent through numerical analysis alone.
- Iterate and Refine: Residual analysis is not a one-time task. Continuously refine your model based on residual findings and re-evaluate as new data becomes available.
Conclusion
Advanced techniques in residual analysis provide valuable insights into complex data trends, allowing analysts to improve model accuracy and interpret results more effectively. By leveraging methods such as quantile regression, smoothing techniques, bootstrap methods, spatial and time-series analysis, you can enhance your understanding of residuals and make more informed decisions based on your data. Embrace these advanced techniques to uncover deeper insights and drive more accurate data analysis outcomes.