In the ever-evolving field of data science, foundational principles play a crucial role in driving innovation and shaping new methodologies. Among these principles, the Law of Large Numbers (LLN) stands out as a pivotal concept that continues to influence the development of data science techniques and technologies. As we progress through 2024, understanding how the LLN is impacting data science can provide valuable insights into current trends and future directions. This article explores the significance of the LLN in data science, its application in modern analytics, and the innovations it is fostering.
What is the Law of Large Numbers?
The Law of Large Numbers is a fundamental theorem in probability theory that describes how the average of a large number of independent, identically distributed random variables tends to approximate the expected value as the sample size increases. There are two main versions of the LLN: the Weak Law of Large Numbers and the Strong Law of Large Numbers.
- Weak Law of Large Numbers (WLLN): This version states that the sample average converges in probability to the expected value as the sample size approaches infinity. In other words, for a large enough sample, the sample mean will be close to the population mean with high probability.
- Strong Law of Large Numbers (SLLN): This version is more stringent and asserts that the sample average almost surely converges to the expected value as the sample size grows. This implies that, with probability 1, the sample mean will eventually be equal to the population mean as the sample size increases.
The Role of LLN in Data Science
In the realm of data science, the LLN has profound implications for statistical inference, machine learning, and predictive modeling. Here’s how it is shaping innovations in these areas:
1. Enhanced Predictive Analytics
Predictive analytics relies heavily on the ability to generalize findings from sample data to the larger population. The LLN ensures that with a sufficiently large dataset, predictions made from sample data will closely reflect the true characteristics of the population. This principle underpins the reliability of various predictive models, such as regression analysis and time series forecasting. As data collection methods become more sophisticated and datasets grow larger, the LLN helps enhance the accuracy of predictions and improves the robustness of predictive models.
2. Improved Machine Learning Algorithms
Machine learning algorithms, especially those involving large datasets, benefit greatly from the LLN. For instance, in ensemble learning techniques like bagging and boosting, multiple models are trained on different subsets of data. The LLN suggests that averaging the predictions from these models will converge to a more accurate result as the number of models increases. This principle is integral to algorithms such as Random Forests and Gradient Boosting Machines, which perform better with larger datasets and more iterations.
3. Refinement of Statistical Testing
Statistical tests, which are used to make inferences about populations based on sample data, are fundamentally supported by the LLN. The accuracy and reliability of hypothesis testing and confidence intervals improve with larger sample sizes, as the LLN ensures that sample statistics become more representative of the population parameters. This refinement in statistical testing contributes to more precise and trustworthy conclusions drawn from data analysis.
4. Advancements in Big Data Analytics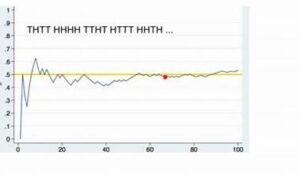
The rise of big data has introduced new challenges and opportunities for data science. The LLN plays a critical role in managing and analyzing massive datasets. As big data technologies and tools handle increasingly larger volumes of data, the LLN helps ensure that data-driven insights are consistent and reliable. This is crucial for applications such as real-time analytics, recommendation systems, and anomaly detection, where large-scale data processing is essential.
Innovations Driven by LLN in 2024
In 2024, the influence of the LLN on data science is manifested through several key innovations:
1. AI and Deep Learning Models
Artificial Intelligence (AI) and Deep Learning (DL) models are increasingly dependent on large datasets for training and validation. The LLN supports the effectiveness of these models by guaranteeing that larger training datasets lead to better generalization and accuracy. Innovations in AI, such as natural language processing and image recognition, are benefiting from this principle, resulting in more powerful and precise models.
2. Real-Time Data Processing
Advancements in real-time data processing technologies are leveraging the LLN to deliver accurate and timely insights. Techniques such as streaming analytics and event-driven architectures are designed to handle vast amounts of data in real time. The LLN ensures that even with continuous data influx, the analysis remains reliable and consistent.
3. Automated Data Cleaning and Validation
Automated data cleaning and validation tools are becoming more sophisticated, thanks to the LLN. These tools utilize large sample sizes to detect and correct errors, inconsistencies, and anomalies in datasets. By applying LLN principles, these tools enhance the quality of data and improve the overall accuracy of data-driven decisions.
4. Enhanced Personalization Algorithms
Personalization algorithms, used in various domains such as e-commerce and content recommendations, are benefiting from the LLN. By analyzing large volumes of user data, these algorithms provide more accurate and relevant recommendations. The LLN ensures that personalization models are robust and reflect the true preferences and behaviors of users.
Conclusion
The Law of Large Numbers continues to be a cornerstone of data science, driving innovations and advancements in the field. As we navigate through 2024, its influence on predictive analytics, machine learning, statistical testing, and big data analytics remains profound. By understanding and applying the LLN, data scientists can enhance the accuracy, reliability, and effectiveness of their models and techniques. As data science evolves, the LLN will undoubtedly play a crucial role in shaping its future developments and innovations.



